Use the next free Laplace inverse calculator to solve problems and check your answers. It has three input fields:
- Field 1: add your function and you can use parameters like \displaystyle\frac{a}{s+b}
- Field 2: specify the Laplace variable which is s in the above example
- Field 3: specify the time variable, t in this case.
Illustrative example about how to use Laplace inverse calculator
As an example, let’s consider the following problem:
Find the inverse Laplace Transform of \displaystyle F(s)=\frac{8}{s+3}.
1. Using the Laplace inverse calculator
- Write the above function in the corresponding field. The function depends on s and we consider t as the time variable. Check the following screenshot:
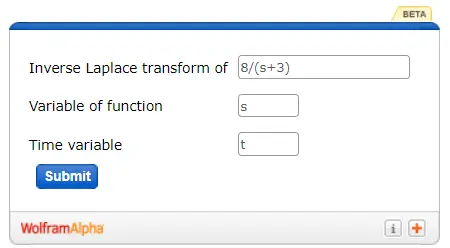
- Then, hit the Submit button to get the following:
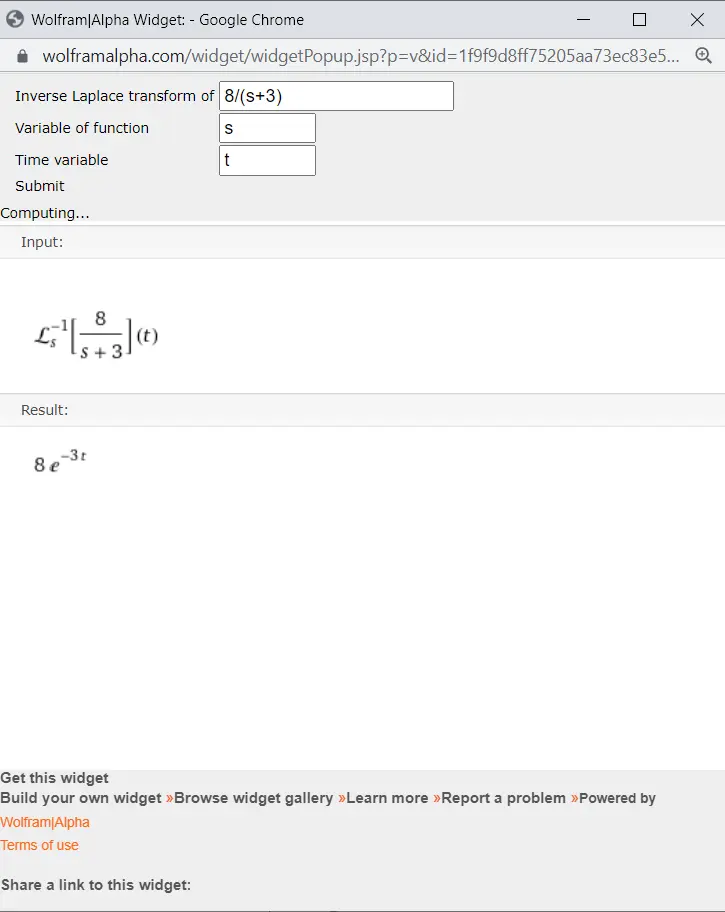
Hence the inverse Laplace transform of \displaystyle F(s)=\frac{8}{s+3} is given by:
\displaystyle f(t)=8 e^{-3t}
2. Using the inverse Laplace transform definition
From the table of Laplace transforms, we have:
\displaystyle \mathscr{L}^{-1}\left\{\frac{1}{s-a}\right\}=e^{at}
In our example, we have a=-3, hence:
\displaystyle \mathscr{L}^{-1}\left\{\frac{1}{s+3}\right\}=e^{-3t}
On the other hand, we have the Linearity property:
\displaystyle \mathscr{L}^{-1}\left\{\frac{8}{s+3}\right\}= 8\mathscr{L}^{-1}\left\{\frac{1}{s+3}\right\}
This means that:
\displaystyle f(t)= 8e^{-3t}
which is the same as the one provided by the inverse Laplace transform calculator!
This calculator widget has been developed by tjmakela in wolframalpha.com
